Zagadka z klientem

Zagadka z klientem i kasjerem. Wyznaczenie cen czterech produktów z warunkiem. Układ równań z czterema niewiadomymi.

Kasjer pomylił się w sklepie i swojemu klientowi zamiast dodać ceny czterech produktów, to pomnożył, prosząc o zapłatę 7,11 zł. Klient, to zauważył i poprosił kasjera o zsumowanie tych cen. Zdziwienie klienta było wielkie bo suma jednak też dała 7,11 zł. Ile kosztowały produkty?

Zakładamy, że każda cena tych produktów dzieli cenę całkowitą bez reszty (0,01).

I sposób

Rozwiązanie:

Otrzymujemy układ równań z czterema niewiadomymi.

Z powyższego układu równań wynika jaką wartość musi spełniać suma dwóch cen produktów (zał. cena produktu c i d).

Ceny poszczególnych produktów muszą dzielić sumę cen tych produktów tj. 7,11.

Pierwszym warunkiem jest znalezienie tych cen dla których iloraz 7,11 przez cenę dowolnego produktu dzieli się bez reszty i otrzymujemy zapis dziesiętny 0,01 lub 0,1. Zatem cd należy do przedziału <0,01; 7,11>.

Wyznaczamy dzielniki wymierne sumy cen produktów 7,11. Kolorem niebieskim zaznaczono ceny, które są dzielnikami wymiernymi sumy cen produktów.
Wartość delty jest większa lub równa 0 wtedy i tylko wtedy, gdy od wartości 7,11 odejmiemy czwartą kolumnę. Suma cen dwóch produktów (zał. ceny produktów c i d) musi być mniejsza niż w czwartej kolumnie.
Jeśli delta jest większa lub równa 0, to możemy wyznaczyć cenę produktu c z podanej nierówności. Znajdziemy wtedy przedział do którego należy cena produktu c. Rozpatrujemy wszystkie możliwości ceny produktu c, co jeden grosz. Jest tylko 10 przykładów, które spełniają powyżej opisane warunki.

Z powyższych obliczeń wyznaczono przedziały do których należy cena produktu c. Zatem uwzględniamy możliwości tej ceny co jeden grosz. Zatem c jest parametrem liczbowym należącym do wskazanych przedziałów powyżej.

Obliczamy ze wzoru:

∆= [7,11 – (c+d)]²- 28,44/cd

a₁={[7,11 – (c+d)] - √[7,11 – (c+d)² – 28,44/cd]}/2
a₂={[7,11 – (c+d)] + √[7,11 – (c+d)² – 28,44/cd]}/2
b₁=[7,11 – (c+d)] – a₁
b₂=[7,11 – (c+d)] – a₂

Ceny produktów wynoszą 1,5; 1,25; 1,2; 3,16.
Sprawdzamy warunki zadania:

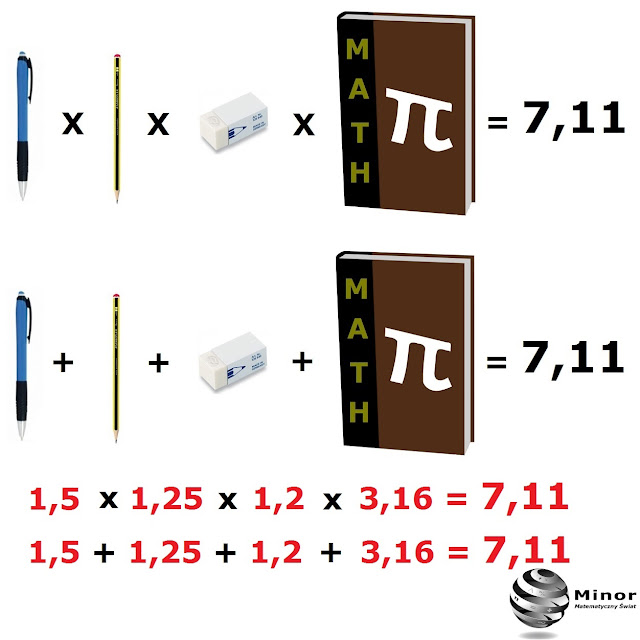
1,5 + 1,25 + 1,2 + 3,16 = 7,11 zł

1,5 · 1,25 · 1,2 · 3,16 = 7,11 zł

W zadaniu należało policzyć ceny produktów, a nie poszczególnych produktów.

II sposób

Rozwiązanie zagadki bez użycia programu:

Post nr 356

Brak komentarzy:

Prześlij komentarz

Regulamin bloga

Czytelniku, miło kiedy komentujesz posty. Chętnie zapoznam się także z innym Twoim punktem widzenia w podanym rozwiązaniu zadania. Jednak, aby ten blog stanowił dla Czytelników pewną wartość, nie mogę pozwolić, żeby każdy mógł tu pisać co tylko chce.

Blog wymaga wiele czasu pracy, godzin pracy, których nie widać i jako jego autor chcę się na nim dobrze czuć. Niniejszy Regulamin określa zasady korzystania z bloga www.matematyczny-swiat.pl. Korzystanie z bloga oznacza akceptację Regulaminu.

Sprawy organizacyjne

1. Jeżeli uważasz, że w jakimś temacie czujesz się bardziej kompetentny, to napisz jak to wygląda z Twojego punktu widzenia.

2. Myśl zanim coś napiszesz – zanim zechcesz skrytykować moje sposoby rozwiązania zadań zastanów się jak możesz z tego skorzystać. Jeszcze raz – nie twierdzę, że wszystko co napiszę będzie dla Ciebie pomocne. Niemniej niektóre wskazówki po Twojej modyfikacji mogą dobrze Ci służyć. Myśl samodzielnie.

3. Ten blog to miejsce, w którym publikuję wskazówki, które mogą pomóc Czytelnikom zrozumieć i nauczyć się rozwiązywać zadania matematyczne.

4. Dozwolone jest kopiowanie zdjęć z bloga na portale społecznościowe lub inne blogi z bezwzględnym podaniem aktywnego linka do bloga. Niedozwolone jest kopiowanie zdjęć i treści bez podania aktywnego linka.

5. Pamiętaj, żeby w ramach kopiowania zdjęć z bloga korzystać z przycisków udostępniania dostępnych w postach na blogu.

6. Zdjęcia w postach na blogu są mojego autorstwa i własnością intelektualną, a zdjęcia kopiowane na mój blog są zawsze z podaniem źródła.

7. Blog posiada jednego autora. Autorem bloga jest Robert Karolewski.

8. Zabrania się, przerabiania, przystosowywania, usuwania logotypu lub dokonywania jakichkolwiek innych zmian w zdjęciach na potrzeby własnej publikacji i przypisywanie im autorstwa. Dopuszczalne jest na własne potrzeby bez ich publikacji.

9. Wszystkie zdjęcia na blogu mojego autorstwa zawierają logotyp Minor Matematyczny Świat.
10. Przykłady w zadaniach prezentowane na blogu są przygotowane przeze mnie i moją własnością intelektualną. Na blogu również dostępne są przykładowe zadania z jakimi można spotkać się na różnym poziomie nauczania.
11. Rozwiązania wszystkich zadań z arkuszy maturalnych posiadają logotyp wobec tego, że są to moje przykładowe odpowiedzi.

12. Niniejszy regulamin obowiązuje również na wszystkich moich portalach społecznościowych.

13. Korzystanie z bloga w całości jest nieodpłatne i dostępne dla wszystkich Czytelników.

Komentarze

14. Wszystkie komentarze na blogu są moderowane przez autora bloga.

a) Jeśli komentarze są obraźliwe zarówno w stosunku do mnie jak i do innych Czytelników, to zostaną usunięte lub ukryte.

b) Jeśli komentarze są niezwiązane z tematem wpisu, to zostaną usunięte lub ukryte.

c) Jeśli komentarze są spamem. Za spam uznaję linki do innych stron, podpisywanie się adresem www, dodawanie adresu strony pod komentarzem, reklama, to zostaną usunięte lub ukryte.

Osoby, które nie będą stosowały się do powyższych zasad $2 mają gwarancję, że ich komentarz nie pojawi się na blogu.

Blog matematyczny Minor | Matematyka

Strony

Łączna liczba wyświetleń

Pomoce dla klasy

Szukaj na tym blogu lub wpisz post nr 1-534