Liczby koliste
Kolejne liczby koliste to 1/7, 1/17, 1/19, 1/23, 1/29, 1/47, 1/59, 1/61, 1/97, 1/109, 1/113, 1/131, 1/149, 1/167, 1/179, 1/181, 1/193, 1/223, 1/229, 1/233, 1/257, 1/263, 1/269, 1/313, 1/337, 1/367, …
Dla 1/7 = 0,(142857) można również zauważyć, że:
142+857=999
714+285=999
571+428=999
857+142=999
285+714=999
428+571=999
oraz
124+875=999
741+258=999
517+482=999
875+124=999
258+741=999
482+517=999
14+28+57=99
71+42+85=99+99
57+14+28=99
85+71+42=99+99
28+57+14=99
42+85+71=99+99
Iloczyny złożone z tych samych cyfr:
142857 ∙ (7 ∙ 1)/9 = 111111
142857 ∙ (7 ∙ 2)/9 = 222222
142857 ∙ (7 ∙ 3)/9 = 333333
142857 ∙ (7 ∙ 4)/9 = 444444
142857 ∙ (7 ∙ 5)/9 = 555555
142857 ∙ (7 ∙ 2)/9 = 222222
142857 ∙ (7 ∙ 3)/9 = 333333
142857 ∙ (7 ∙ 4)/9 = 444444
142857 ∙ (7 ∙ 5)/9 = 555555
142857 ∙ (7 ∙ 6)/9 = 666666
142857 ∙ (7 ∙ 7)/9 = 777777
142857 ∙ (7 ∙ 8)/9 = 888888
142857 ∙ (7 ∙ 9)/9 = 999999
142857 ∙ (7 ∙ 9)/9 = 999999
Iloczyny kolejnych cyfr 142857 i 7 dopełnione w odpowiedniej kolejności liczbami z zakresu 1, ..., n-1 tj. 3, 2, 6, 4, 5, 1 dają kolejne potęgi naturalne liczby 10:
1 ∙ 7 + 3 = 10
14 ∙ 7 + 2 = 100
142 ∙ 7 + 6 = 1000
1428 ∙ 7 + 4 = 10000
14285 ∙ 7 + 5 = 100000
142857 ∙ 7 + 1 = 1000000
1428571 ∙ 7 + 3 = 10000000
14285714 ∙ 7 + 2 = 100000000
142857142 ∙ 7 + 6 = 1000000000
1428571428 ∙ 7 + 4 = 10000000000
14285714285 ∙ 7 + 5 = 100000000000
142857142857 ∙ 7 + 1 = 1000000000000
Większe liczby koliste to 1/1861, 1/7699, 1/17389.
Hipotetycznie uznajemy, że liczb kolistych jest nieskończenie wiele. Ułamek liczb kolistych przypadający na wszystkie liczby pierwsze zawarte w określonym przedziale zbiega się do stałej Artina, CA=0,3739558136…
1 ∙ 7 + 3 = 10
14 ∙ 7 + 2 = 100
142 ∙ 7 + 6 = 1000
1428 ∙ 7 + 4 = 10000
14285 ∙ 7 + 5 = 100000
142857 ∙ 7 + 1 = 1000000
1428571 ∙ 7 + 3 = 10000000
14285714 ∙ 7 + 2 = 100000000
142857142 ∙ 7 + 6 = 1000000000
1428571428 ∙ 7 + 4 = 10000000000
14285714285 ∙ 7 + 5 = 100000000000
142857142857 ∙ 7 + 1 = 1000000000000
Większe liczby koliste to 1/1861, 1/7699, 1/17389.
Hipotetycznie uznajemy, że liczb kolistych jest nieskończenie wiele. Ułamek liczb kolistych przypadający na wszystkie liczby pierwsze zawarte w określonym przedziale zbiega się do stałej Artina, CA=0,3739558136…
gdzie pk to kolejne liczby pierwsze.


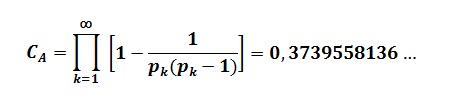
Brak komentarzy:
Prześlij komentarz