Tweety na temat @MinorMatematyka

Łączna liczba wyświetleń

Snapchat: matematycznyswi

Snapchat: matematycznyswi

Szukaj na tym blogu lub wpisz post nr 1-524

środa, 30 lipca 2014

Wielościany foremne, bryły platońskie

Wielościany foremne, bryły platońskie

 

Wielościany foremne, bryły platońskie
                                               Źródło: Animacja Walter Fendt


Wielościan foremny (bryła platońska) – wielościan spełniający następujące trzy warunki:
Wielościany foremne są szczególnym przypadkiem wielościanów półforemnych (archimedesowskich), w których foremne ściany nie muszą być identyczne (tj. wzajemnie przystające).
Wielościanem foremnym (bryłą platońską) nazywamy wielościan wypukły, którego wszystkie ściany są  przystającymi wielokątami foremnymi i wszystkie katy dwuścienne wyznaczone przez ściany są równe.
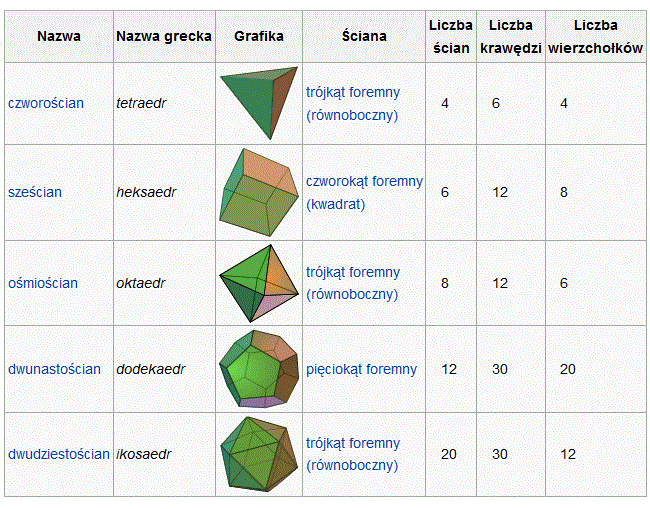
Istnieje tylko pięć wielościanów foremnych - czworościan, sześcian, ośmiościan, dwunastościan, dwudziestościan.

Czworościan (tetraedr)
4 ściany trójkątne, 4 wierzchołki, 6 krawędzi.
Każda z jego ścian jest trójkątem równobocznym. Jest on szczególnym przypadkiem ostrosłupa prawidłowego trójkątnego.
  

Sześcian (heksaedr)
6 ścian kwadratowych, 8 wierzchołków, 12 krawędzi.
Sześcian foremny to wielościan foremny o sześciu ścianach w kształcie identycznych kwadratów. Kąt między ścianami sześcianu jest kątem prostym. Sześcian foremny jest szczególnym przypadkiem graniastosłupa prawidłowego, prostopadłościanu i romboedru.


Ośmiościan (oktaedr)
8 ścian trójkątnych, 6 wierzchołków, 12 krawędzi.
Ośmiościan foremny to wielościan foremny o ośmiu ścianach w kształcie identycznych trójkątów równobocznych. Ma cztery pary ścian do siebie równoległych. Jest także antygraniastosłupem.


Dwunastościan (dodekaedr)
12 ścian pięciokątnych, 20 wierzchołków, 30 krawędzi.

Dwudziestościan (ikosaedr)
20 ścian trójkątnych, 12 wierzchołków, 30 krawędzi

Dlaczego wielościanów foremnych nie może być więcej niż pięć?
Suma wszystkich kątów płaskich kąta bryłowego musi być mniejsza od 360°.

Z trójkątów można zbudować trzy wielościany foremne, gdzie z jednego wierzchołka mogą wychodzić:
- 3 krawędzie (60° × 3 = 180° < 360°)
- 4 krawędzie (60° × 4 = 240° < 360°)
- 5 krawędzi (60° × 5 = 300° < 360°).

Z kwadratów składać się może tylko jeden wielościan (3 × 90° = 270°).

Z pięciokątów foremnych składać się może również tylko jeden, gdyż kąt pięciokąta foremnego ma miarę 108°  (3 × 108° < 360°).

Z sześciokątów, ani tym bardziej z wielokątów o większej liczbie boków, wielościanu foremnego zbudować się nie można.  

Wielościany foremne w przestrzeni trójwymiarowej:
Wielościany foremne, bryły platońskie
 
 Źródło: Zdjęcie Wikipedia


Wielościany foremne, bryły platońskie



Post nr 438
Autor: o
Etykiety: , ,

Liczba komentarzy:
Reakcje: 

Brak komentarzy:

Prześlij komentarz

Subskrybuj: Komentarze do posta (Atom)

Regulamin bloga

Czytelniku, miło kiedy komentujesz posty. Chętnie zapoznam się także z innym Twoim punktem widzenia w podanym rozwiązaniu zadania. Jednak, aby ten blog stanowił dla Czytelników pewną wartość, nie mogę pozwolić, żeby każdy mógł tu pisać co tylko chce.

Blog wymaga wiele czasu pracy, godzin pracy, których nie widać i jako jego autor chcę się na nim dobrze czuć. Niniejszy Regulamin określa zasady korzystania z bloga www.matematyczny-swiat.pl. Korzystanie z bloga oznacza akceptację Regulaminu.



$1

Sprawy organizacyjne

1. Jeżeli uważasz, że w jakimś temacie czujesz się bardziej kompetentny, to napisz jak to wygląda z Twojego punktu widzenia.

2. Myśl zanim coś napiszesz – zanim zechcesz skrytykować moje sposoby rozwiązania zadań zastanów się jak możesz z tego skorzystać. Jeszcze raz – nie twierdzę, że wszystko co napiszę będzie dla Ciebie pomocne. Niemniej niektóre wskazówki po Twojej modyfikacji mogą dobrze Ci służyć. Myśl samodzielnie.

3. Ten blog to miejsce, w którym publikuję wskazówki, które mogą pomóc Czytelnikom zrozumieć i nauczyć się rozwiązywać zadania matematyczne.

4. Dozwolone jest kopiowanie zdjęć z bloga na portale społecznościowe lub inne blogi z bezwzględnym podaniem aktywnego linka do bloga. Niedozwolone jest kopiowanie zdjęć i treści bez podania aktywnego linka.

5. Pamiętaj, żeby w ramach kopiowania zdjęć z bloga korzystać z przycisków udostępniania dostępnych w postach na blogu.

6. Zdjęcia w postach na blogu są mojego autorstwa i własnością intelektualną, a zdjęcia kopiowane na mój blog są zawsze z podaniem źródła.

7. Blog posiada jednego autora. Autorem bloga jest Robert Karolewski.

8. Zabrania się, przerabiania, przystosowywania, usuwania logotypu lub dokonywania jakichkolwiek innych zmian w zdjęciach na potrzeby własnej publikacji i przypisywanie im autorstwa. Dopuszczalne jest na własne potrzeby bez ich publikacji.

9. Wszystkie zdjęcia na blogu mojego autorstwa zawierają logotyp Minor Matematyczny Świat.
10. Przykłady w zadaniach prezentowane na blogu są przygotowane przeze mnie i moją własnością intelektualną. Na blogu również dostępne są przykładowe zadania z jakimi można spotkać się na różnym poziomie nauczania.
11. Rozwiązania wszystkich zadań z arkuszy maturalnych posiadają logotyp wobec tego, że są to moje przykładowe odpowiedzi.

12. Niniejszy regulamin obowiązuje również na wszystkich moich portalach społecznościowych.

13. Korzystanie z bloga w całości jest nieodpłatne i dostępne dla wszystkich Czytelników.


$2

Komentarze

14. Wszystkie komentarze na blogu są publikowane automatycznie i moderowane przez autora bloga.

a) Jeśli komentarze są obraźliwe zarówno w stosunku do mnie jak i do innych Czytelników, to zostaną usunięte lub ukryte.

b) Jeśli komentarze są niezwiązane z tematem wpisu, to zostaną usunięte lub ukryte.

c). Jeśli komentarze są spamem. Za spam uznaję linki do innych stron, podpisywanie się adresem www, dodawanie adresu strony pod komentarzem, reklama, to zostaną usunięte lub ukryte.


Osoby, które nie będą stosowały się do powyższych zasad $2 mają gwarancję, że ich komentarz pojawi się chwilę na blogu. W skrajnych przypadkach Twoje konto zostanie zablokowane.