Zaznaczanie punktów w prostokątnym układzie współrzędnych
Prostokątnym układem współrzędnych nazywamy dwie prostopadłe osie liczbowe (oś liczbowa jest to prosta na której zaznaczono jednostkę, punkt zerowy 0 i zwrot) przecinające się punkcie, któremu na obu osiach odpowiada liczba 0.
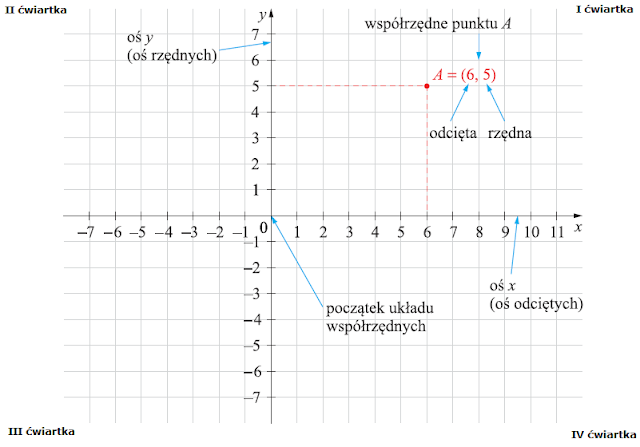
Punkt przecięcia osi nazywamy początkiem układu współrzędnych, oznaczamy O i zapisujemy O = (0, 0).
Położenie każdego punktu na płaszczyźnie określa para liczb zwana współrzędnymi punktu. Pierwszą liczbę odczytujemy z osi x (poziomej), a drugą z osi y (pionowej). Oś x nazywamy też osią odciętych, a oś y osią rzędnych. Współrzędne punkty (x, y) nazywamy odpowiednio odciętą i rzędną tego punktu.
Osie układu współrzędnych dzielą płaszczyznę na cztery części, które nazywamy ćwiartkami układu współrzędnych.
Układ współrzędnych, w których osie są prostopadłe, nazywamy inaczej układem współrzędnych kartezjańskich. Nazwa pochodzi od francuskiego matematyka i filozofa, Kartezjusza.
Każdy punkt (x, y) w prostokątnym układzie współrzędnych można zaznaczyć:
współrzędną x - wyznacz prostą prostopadłą do osi x w punkcie (x, 0);
współrzędną y - wyznacz prostą prostopadłą do osi y w punkcie (0, y).
Punkt przecięcia się tych prostych wyznacza współrzędne punktu A = (x, y).
Instrukcja
Zaznaczanie punktów w prostokątnym układzie współrzędnych w GeoGebrze
Obrazek 1
W prostokątnym układzie współrzędnych zaznacz kolejne punkty wielokąta.
(-4, 2), (-3, 5), (-2, 4), (-2, 5), (0, 3), (0, 1), (1, 0), (5, 1), (8, 5), (5, 0), (4, -5), (3, -5), (3, -3), (2, -2), (1, -2), (1, -5), (0, -5), (0, -2), (-1, -2), (-1, -5), (-2, -5), (-2, -2), (-2, 0), (-4, 2)
Obrazek to: ...................................
Obrazek 2
W prostokątnym układzie współrzędnych zaznacz kolejne punkty wielokąta.
(2, 4), (1, 6), (2, 6), (2, 5), (4, 5), (4, 3), (2, 3), (2, 0), (3, 0), (4, -2), (2, -2), (0, 0), (-3, 0), (-5, -2), (-5, -4), (-7, -2), (-5, 0), (-5, 2), (-7, 4), (-5, 3), (0, 3), (2, 4)
Obrazek to: ...................................
Obrazek 3
W prostokątnym układzie współrzędnych zaznacz kolejne punkty wielokąta.
(-1,
5), (3, 5), (5, 3), (4, 3), (4, -1), (2,
-1), (2, 1), (-2, 1), (-2, -1), (-4, -1), (-4, 2), (-5, 3), (-7, 2), (-8, 2),
(-9, 3), (-9, 4), (-8, 3), (-7, 3), (-6, 4), (-5, 6), (-4, 7), (-2, 7), (-1, 5)
Obrazek to: ...................................
Obrazek 4
W prostokątnym układzie współrzędnych zaznacz kolejne punkty wielokąta.
W prostokątnym układzie współrzędnych zaznacz kolejne punkty wielokąta.
(-2, 5), (-5, 2), (-3, 2), (-2, 1), (-7, 1),
(-7, 0), (-3, 0), (-3, -6), (-2, -6), (-2, -3), (-1, -3), (-1, -6), (0, -6), (0, 0),
(4, 0), (4, 1), (-1, 1), (0, 2), (2, 2), (-2, 5)
Obrazek to: ...................................
Post nr 510








Brak komentarzy:
Prześlij komentarz