Zamiana postaci ogólnej na kanoniczną i postaci kanonicznej na ogólną funkcji homograficznej
Algorytm I
Algorytm II
Zamiana
postaci ogólnej na postać kanoniczną funkcji homograficznej i postaci
kanonicznej na postać ogólną funkcji homograficznej.
Sprawdźmy wyprowadzony wzór na zamianę postaci ogólnej funkcji homograficznej na postać kanoniczną. Należy sprawdzić czy wykresy funkcji homograficznej zapisane w postaci ogólnej i kanonicznej narysowane w układzie współrzędnych pokrywają się. Wtedy wiemy, że postać kanoniczna została prawidłowo wyznaczona.
I przykład - algorytm I
II przykład - algorytm I

Wykres online
III przykład - algorytm I

Wykres online
III przykład - algorytm II

Wykres online
IV przykład - algorytm I

Wykres online
IV przykład - algorytm II

Wykres online
Wykres funkcji homograficznej jest przesunięciem równoległym pewnej hiperboli i posiada on dwie asymptoty:
- pionową
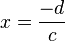 i poziomą
i poziomą 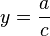 .
.
Punkt 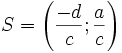 to środek symetrii tego wykresu. Funkcja homograficzna jest monotoniczna na każdym z przedziałów
to środek symetrii tego wykresu. Funkcja homograficzna jest monotoniczna na każdym z przedziałów  oraz
oraz 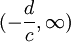 .
.
Funkcja jest:
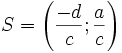 to środek symetrii tego wykresu. Funkcja homograficzna jest monotoniczna na każdym z przedziałów
to środek symetrii tego wykresu. Funkcja homograficzna jest monotoniczna na każdym z przedziałów  oraz
oraz 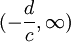 .
.Funkcja jest:
- przedziałami malejąca, gdy
 oraz
oraz - przedziałami rosnąca, gdy
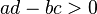 .
.
Wykres funkcji homograficznej 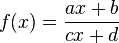 , gdzie
, gdzie  oraz
oraz  powstaje w wyniku przesunięcia równoległego wykresu pewnej hiperboli o pewien wektor. Zauważmy w tym celu, że dla wszystkich
powstaje w wyniku przesunięcia równoległego wykresu pewnej hiperboli o pewien wektor. Zauważmy w tym celu, że dla wszystkich  mamy
mamy
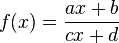 , gdzie
, gdzie  oraz
oraz  powstaje w wyniku przesunięcia równoległego wykresu pewnej hiperboli o pewien wektor. Zauważmy w tym celu, że dla wszystkich
powstaje w wyniku przesunięcia równoległego wykresu pewnej hiperboli o pewien wektor. Zauważmy w tym celu, że dla wszystkich  mamy
mamy
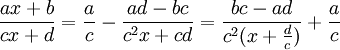 .
.
Zatem wykres funkcji  powstaje w wyniku translacji hiperboli o równaniu
powstaje w wyniku translacji hiperboli o równaniu
 powstaje w wyniku translacji hiperboli o równaniu
powstaje w wyniku translacji hiperboli o równaniu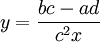 o wektor
o wektor ![\vec{u}=[-\frac{d}{c}, \frac{a}{c}]](https://upload.wikimedia.org/math/2/f/8/2f8176852baf2b325bb5c895ea582bd8.png) .
.
Własności funkcji homograficznej.
Post nr 353











Brak komentarzy:
Prześlij komentarz