Mnożenie logarytmów o różnych podstawach
Wyznacz
wartość wyrażeń x, y, z zapisanych za pomocą logarytmów a następnie oblicz
wartość wyrażenia 48xy√z.
Rozwiązanie I:
Pomiędzy logarytmami o różnych podstawach zachodzi związek:
Obliczamy wartość wyrażenia z:
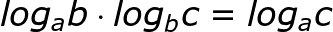
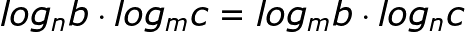
Rozwiązanie w kalkulatorze graficznym. Kliknij na kalkulator w okienku.
Post nr 330
Rozwiązanie I:
Pomiędzy logarytmami o różnych podstawach zachodzi związek:
Obliczamy wartość wyrażenia x:
Obliczamy wartość wyrażenia y:
Obliczamy wartość wyrażenia z:
Rozwiązanie II:
Pomiędzy logarytmami o różnych podstawach zachodzi związek:
Zobacz także jak można mnożyć logarytmy o różnych podstawach jeśli pomiędzy nimi zachodzi związek (więcej).
Pomiędzy logarytmami o różnych podstawach zachodzi związek:
Obliczamy wartość wyrażenia x, y, z wykorzystaniem tych związków:
Zobacz także jak można mnożyć logarytmy o różnych podstawach jeśli pomiędzy nimi zachodzi związek (więcej).
Rozwiązanie w kalkulatorze graficznym. Kliknij na kalkulator w okienku.
Post nr 330
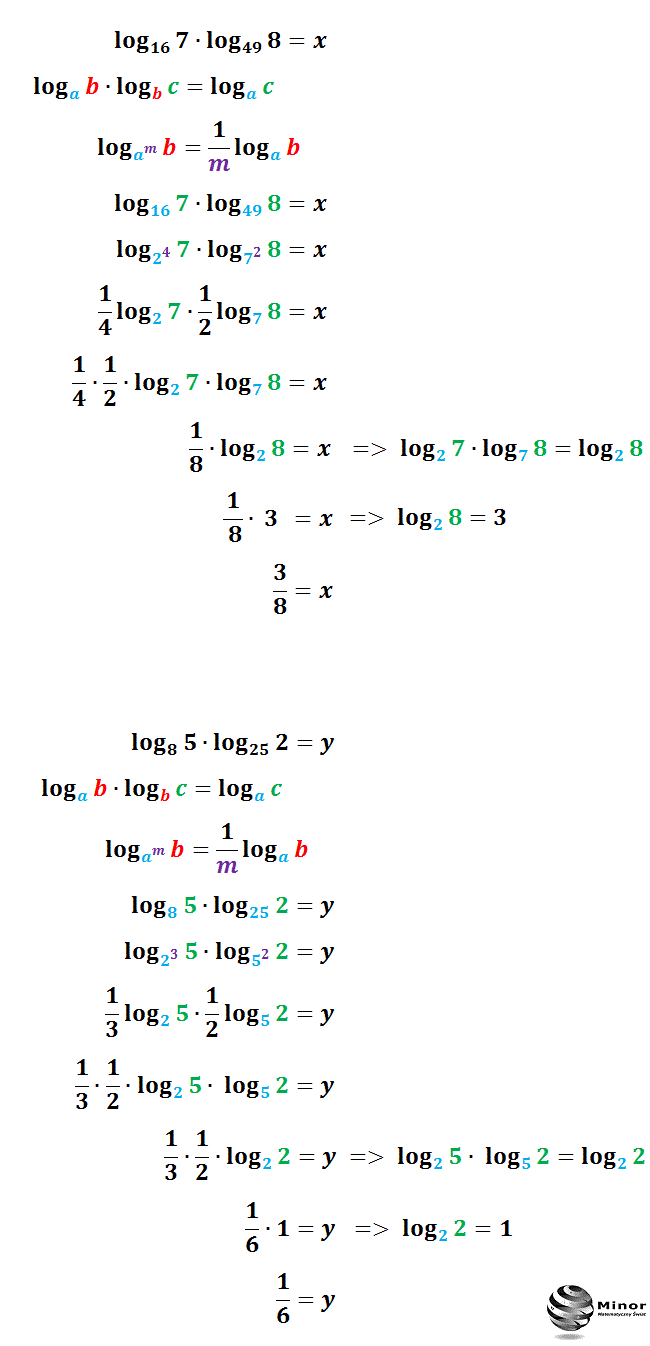
W rozwiązaniu pierwszym na podstawie jakich obliczeń stwierdzono,że b=4 i b=7
OdpowiedzUsuńNa podstawie wzorów, które zapisałem.
Usuń4 dlatego, że podstawa logarytmu jest równa 16. Wiemy, że 16^(1/2)=4 7 dlatego, że podstawa logarytmu jest równa 49. Wiemy, że 49^(1/2)=7 Wniosek: Za literę b możemy podstawić dowolną liczbę, ale żeby była wynikiem potęgowania.
UsuńDzięki za odpowiedź. W mojej opinii, druga wersja rozwiązania jest łatwiejsza ponieważ korzystam ze wzorów i nie muszę zakładać dodatkowych "zmiennych". Zamiast podstawić za 16 = 2^4 można podstawić 4^2.
OdpowiedzUsuń1 zadanie. Dlaczego w 4 linijce liczbą logarytmową jest 4 przy podstawie 16 ?
OdpowiedzUsuńDlatego, że 16^(1/2) = 4.
Usuń