Mnożenie logarytmów o różnych podstawach
Oblicz wartość wyrażenia x, y, z
wykonując działania z mnożeniem logarytmów o różnych podstawach a następnie
oblicz wartość wyrażenia A.
Rozwiązanie:
W podanych działaniach będziemy korzystać
z następującego wzoru z mnożeniem logarytmów o różnych podstawach:
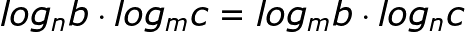
Czynniki
dobieramy odpowiednio tak, żeby można było obliczyć wartość logarytmów wiedząc,
że pomiędzy tymi logarytmami zachodzi powyższy związek.

Zobacz także jak można mnożyć logarytmy o różnych podstawach jeśli pomiędzy nimi zachodzi związek (więcej).
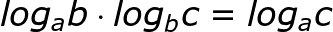

Rozwiązanie w kalkulatorze graficznym. Kliknij na kalkulator w okienku.

Rozwiązanie w kalkulatorze graficznym. Kliknij na kalkulator w okienku.
Post nr 370




Brak komentarzy:
Prześlij komentarz