Równanie pierwiastkowe

Równanie pierwiastkowe z pierwiastkami czwartego stopnia

Wyznacz rozwiązanie równania pierwiastkowego z pierwiastkami czwartego stopnia. 

Rozwiązanie:

- przekształcamy równanie do prostszej postaci

- wprowadzamy pomocniczą t za pierwiastek czwartego stopnia z liczby x

- wyznaczamy rozwiązania równania kwadratowego

- wyznaczamy rozwiązania równania pierwiastkowego

- sprawdzamy rozwiązania równania pierwiastkowego

Wykres online

 

Post nr 494

Równanie odcinkowe prostej

Równanie prostej w postaci ogólnej i kierunkowej, a równanie prostej w postaci odcinkowej

Znając współczynnik kierunkowy (a) prostej i jeden dowolny punkt leżący na prostej (należący do prostej), można wyznaczyć takie równanie prostej:

y-y₁ = a(x-x₁)

Znając dwa dowolne punkty leżące na prostej (należące do prostej) można wyznaczyć takie równanie prostej: y-y₁ = a(x-x₁), gdzie a = (y₂-y₁)/(x₂-x₁)

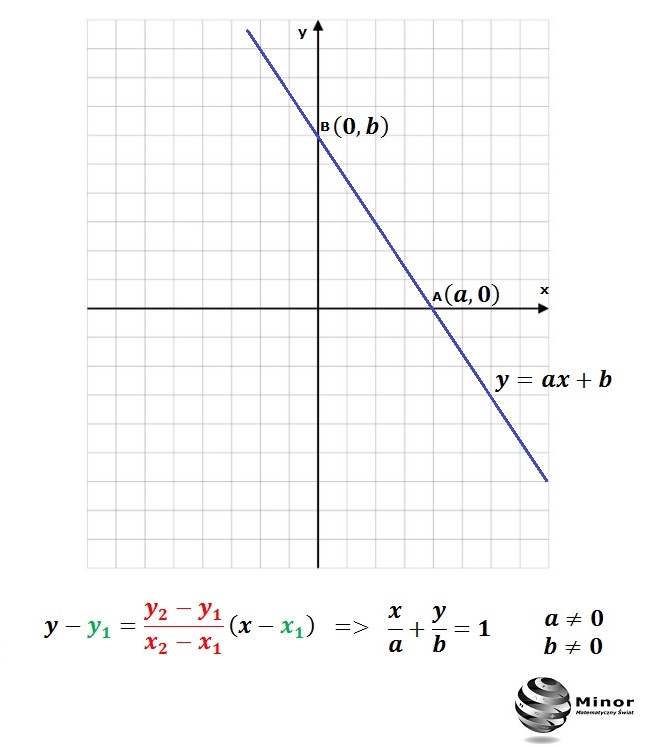
Znając dwa szczególne punkty przecięcia się wykresu z osiami układu współrzędnych OX, OY, można wyznaczyć takie równanie prostej nazywane równaniem odcinkowym prostej.

x/a + y/b = 1, gdzie a≠0, b≠0 i b to współczynnik zaczepienia.

Wyznaczanie wzoru funkcji liniowej do postaci kierunkowej z postaci odcinkowej x/a + y/b = 1 => y = ax +b.

Wyznaczanie wzoru funkcji liniowej do postaci odcinkowej z postaci kierunkowej lub ogólnej y = ax +b lub Ax + By + C =0 => x/a + y/b = 1.

Przykład I

Przykład II

Przykład III

Przykład IV

Post nr 493

Trójkąt prostokątny wpisany w trapez równoramienny

W trapez równoramienny wpisano trójkąt prostokątny

W trapez równoramienny wpisano trójkąt prostokątny w taki sposób, że kąt prosty trójkąta prostokątnego podzielił krótszą podstawę trapezu na odcinki 8 i 3, a przeciwprostokątna trójką prostokątnego zawiera się w dłuższej podstawie trapezu. Wyznacz długość dłuższej podstawy trapezu równoramiennego wiedząc, że wysokość trapezu wynosi 6.

Rozwiązanie:

Post nr 492